本文共 2704 字,大约阅读时间需要 9 分钟。
1.前言
1.1声明
文章中的文字可能存在语法错语以及标点错误,请谅解;
如果在文章中发现代码错误或其它问题请告知,感谢!
2.数据库基本概念
数据库系统是当代计算机系统的重要组成部分,因为几乎所有现行的应用程序都需要存储数据。数据库系统的首要功能就是能借助计算机科学保管大量、各种类型的数据。数据库系统也包括数据处理部分,该部分能够对数据进行收集、存储、检索和维护,目的就是可以从大量原始数据中截取、推导出对使用者有价值的信息作为下一步处理的源信息。
2.1数据与数据库
数据是数据库存储的基本对象,可以是文字或图片声音等,数据库可以理解为计算机上的大容量硬盘,是一个可以表现为多种形式的可共享的数据集合。
2.2数据库管理系统
数据库管理系统(Data Base Management System,DBMS)是位于用户和操作系统之间的数据管理软件,提供对数据库的建立、使用、维护功能。数据库管理系统能够对数据库进行统一的管理和控制。用户可以使用数据库命令和数据库管理系统提供的API来对数据库中的数据进行提取操作。数据库管理系统还承担数据库维护工作。
数据库管理系统有Oracle、Informix、Sybase、MySQL等。本文章以MySQL为例讲述数据库开发的基础知识。2.3数据库语言
数据库语言一般分为两种:交互式命令语言和嵌入到设计语言中的数据库语言(数据库通过提供API函数来实现交互)。
3.MySQL数据库
MySQL数据库具有功能强大、灵活性好、提供丰富API的特点,收到了广大自由软件爱好者的喜爱,特别是与Apache和PHP/PERL组合,为建立基于数据库的动态网站提供了强大支持。
MySQL采用SQL语言标准,关于SQL语句部分,可以参考下面的连接:3.1MySQL安装
在终端上输入指令安装MySQL库:apt-get install mysql-server mysql-client
在安装过程中弹出窗口,设置根用户密码:
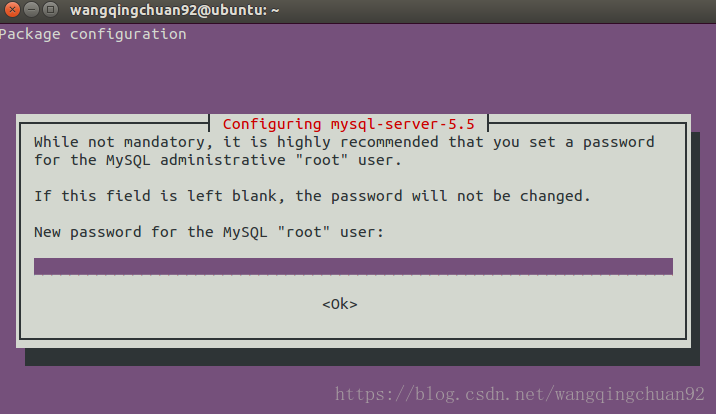
安装结束后,MySQL服务器应该自启动,输入:sudo netstat -tap | grep mysql检查MySQL服务器是否正在运行:
当出现类似下面行表明MySQL服务器已经启动:

若服务器没有启动成功,输入如下指令手工启动:sudo /etc/init.d/mysql restart
在MySQL服务器启动成功后,输入如下指令进入MySQL:mysql -u root -p
 其中,-u为用户名,-p为密码,-p后面的密码可以不在指令中填写,在指令执行后mysql会要求输入密码,当然,使用
其中,-u为用户名,-p为密码,-p后面的密码可以不在指令中填写,在指令执行后mysql会要求输入密码,当然,使用mysql -u root ppassword可直接进入MySQl:  此mysql数据库密码是aabbcc,需要注意的是,这里的语法有一点特殊,-p后面的密码不需要空格隔开。所以最后一个参数的书写形式为-paabbcc。
此mysql数据库密码是aabbcc,需要注意的是,这里的语法有一点特殊,-p后面的密码不需要空格隔开。所以最后一个参数的书写形式为-paabbcc。 此时系统提示输入密码,密码为在安装过程中设定的密码,输入密码之后进入MySQl:
在mysql提示符后面输入quit便可以退出MySQL:

3.2MySQL管理
除了上述mysql -u root -p,MySQL自带其它少量管理指令,在编写访问MySQL程序之前,可以简要了解一下:
所有指令都有3个标准参数: -u Username -p[Password] -h host
-u后面的参数为MySQL用户名,-p后面的参数为密码,若不在指令中给出,则进入MySQL会提示输入密码,-h后面的参数用于在不同主机上连接一台服务器,对于本地服务器则此参数可以省略。1.mysqladmin
mysqladmin为主要的管理指令,该指令有几个主要命令选项:| create dbname |创建一个名为dbname的新数据库 |
| drop dbname | 删除dbname数据库 | | flush-tables | 清洗所有列表 | | password newpassword | 用newpassword变更原有口令 | | shutdown | 关掉MySQL服务器 | | status | 给出服务器的简短状态信息 | | variables | 打印所有可用变量 | | version | 给出服务器的版本信息 |举例:
查看服务器状态:$sudo mysqladmin -u root -p status
2.mysqldump
mysqldump指令可以将数据库(所有或选定的表)导出到一个文件中,一般用作备份,该指令有几个主要命令选项:| - -add-locks | 在每个表导出之前增加LOCK TABLES并且之后UNLOCK TABLE |
| - -add-drop-table | 在每个create语句之前增加一个drop table | | - -allow-keywords | 允许创建时关键词的列的名字 | | -c, - -complete-insert | 使用完整的insert语句 | | -C,- -compress | 如果客户和服务器均支持压缩,压缩两者之间的所有信息 | | - -delayed | 用INSERT DELAYED 命令插入行 | | -d,- -no-data | 不写入表的任何行信息,只导出表结构 | | -t,- -no-create-info | 不写入表创建信息(CREATE TABLE语句) | | - -help | 显示帮助信息 |举例:
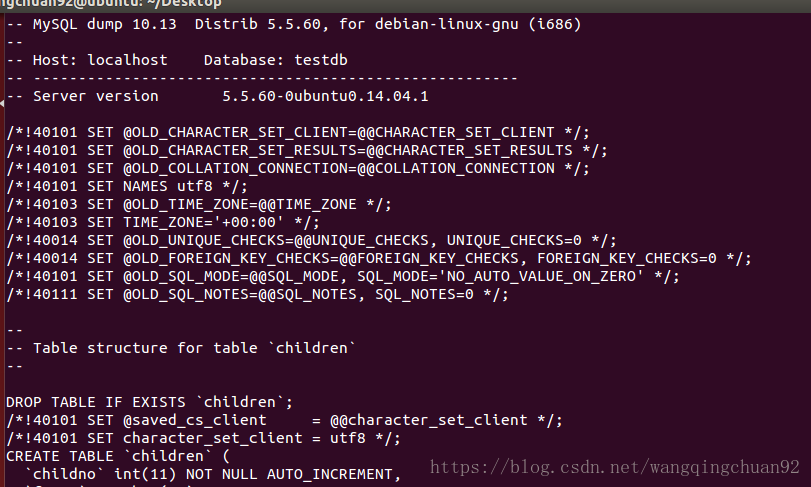
将数据库mysql导出到文件test.bak中:$mysqldump -u root -p mysql>/home/wangqingchuan92/Desktop/test.bak
3.mysqlshow
根据设定的参数显示服务器、数据库或者表的信息: (1)没有参数时,列出所有可用的数据库; (2)参数是一个数据库时,列出数据库中所有的表; (3)参数是一个数据库及一个表的名称时,列出指定列的信息; (4)参数是数据库、表和列时,列出制定列的信息。举例1:
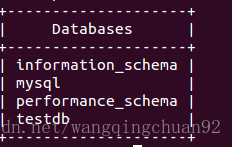
显示所有数据库:$mysqlshow -u root -p
举例2:
显示数据库testdb中所有表:$mysqlshow -u root -p testdb
举例3:
显示testdb中的children表:$mysqlshow -u root -p testdb children

参考资料:
刘学勇.Linux C编程从入门到精通[M].北京,电子工业出版社,2014.1.